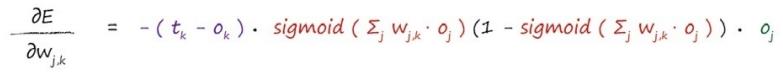学习及原理

学习

读书笔记：https://1keven1.github.io/2023/07/24/%E3%80%90%E8%AF%BB%E4%B9%A6%E7%AC%94%E8%AE%B0%E3%80%91Python%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C%E7%BC%96%E7%A8%8B/

原理

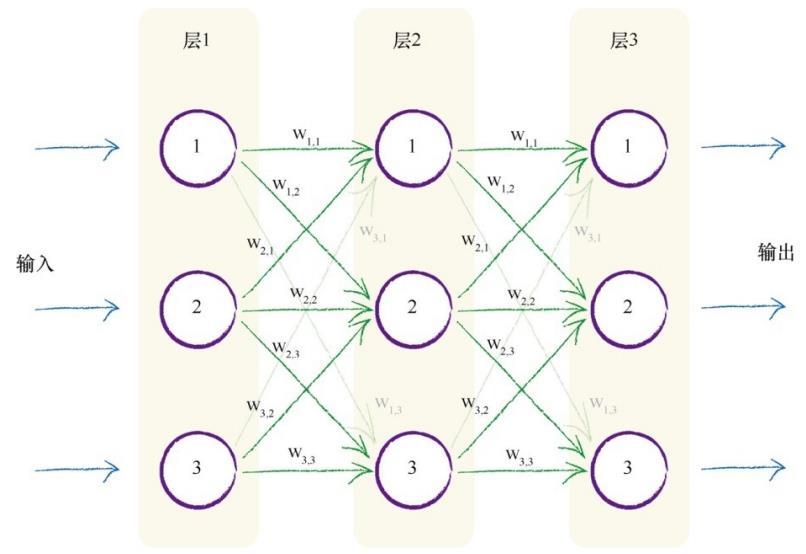
  1. 使用三层神经网络（输入层、隐藏层、输出层）。

    神经网络示例

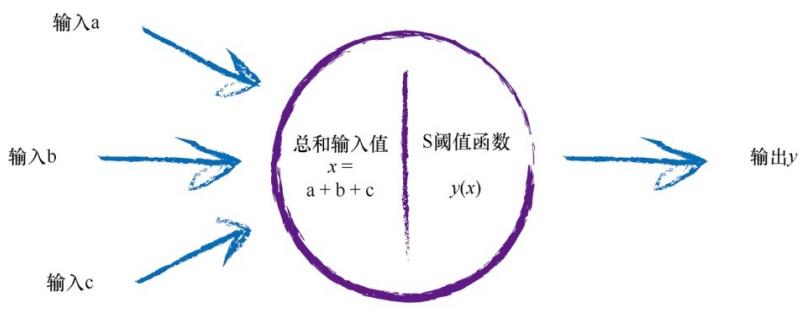
  2. 输入训练集数字的28*28亮度值，根据权重计算每个节点的值。

    单个神经元逻辑示例

  3. 输出为10个节点，预期输出为对应数字的节点为0.99，其它节点为0.01。

  4. 根据实际输出与预期输出，计算权重变化梯度，找到梯度为负的方向并前进（梯度下降）。

    梯度公式

  5. 根据梯度方向和学习率更新权重

其中，计算可以使用大矩阵乘法简化运算。

实现

Neural Network类

在初始化函数中，应用输入、隐藏、输出层节点数量。

初始化权重矩阵：随机值，范围为节点传入链接数量的平方根倒数。

设置激活函数和其逆函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy
import scipy.special    # sigmoid函数


# 神经网络类
class NeuralNetwork:
    """简单三层神经网络类

    输入层、隐藏层和输出层
    """
    def __init__(self, input_num, hidden_num, output_num):
        self.i_num = input_num
        self.h_num = hidden_num
        self.o_num = output_num
        # 权重矩阵
        # 正态分布
        self.wih = numpy.random.normal(0.0, pow(self.h_num, -0.5), (self.h_num, self.i_num))
        self.who = numpy.random.normal(0.0, pow(self.o_num, -0.5), (self.o_num, self.h_num))

        # 激活函数
        self.activation_func = lambda x: scipy.special.expit(x)
        self.inverse_activation_func = lambda x: scipy.special.logit(x)
        pass
    	
    # 训练
    def train(self, inputs_list, targets_list, lr):
        pass

    # 查询
    def query(self, inputs):
        return final_outputs
    
    pass

下面实现train和query函数

训练

传入输入节点值和预期值的列表，转换成numpy数组后，就可以使用numpy的矩阵乘法进行运算了。

根据公式算出误差梯度，并更新权重。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 训练
def train(self, inputs_list, targets_list, lr):
    # 转换成数组
    inputs = numpy.array(inputs_list, ndmin=2).T
    targets = numpy.array(targets_list, ndmin=2).T

    # 隐藏层
    hidden_outputs = self.activation_func(numpy.dot(self.wih, inputs))

    # 输出层
    final_outputs = self.activation_func(numpy.dot(self.who, hidden_outputs))

    # 误差
    output_errors = targets - final_outputs
    hidden_errors = numpy.dot(self.who.T, output_errors)

    # 更新权重
    self.who += lr * numpy.dot((output_errors * final_outputs * (1 - final_outputs)), hidden_outputs.T)
    self.wih += lr * numpy.dot((hidden_errors * hidden_outputs * (1 - hidden_outputs)), inputs.T)
    pass

查询

查询比较简单，只要根据传入的输入值，难过神经网络计算出输出值即可：

1
2
3
4
5
6
7
8
9
# 查询
def query(self, inputs):
    # 输入层->隐藏层
    hidden_inputs = numpy.dot(self.wih, inputs)
    hidden_outputs = self.activation_func(hidden_inputs)
    # 隐藏层->输出层
    final_inputs = numpy.dot(self.who, hidden_outputs)
    final_outputs = self.activation_func(final_inputs)
    return final_outputs

测试

训练集、测试集下载：https://pjreddie.com/projects/mnist-in-csv/

训练后使用测试集进行测试，为了效率，先将隐藏层节点数量设小（100），epochs为1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import numpy
import NeuralNetwork


# 训练参数
training_file_loc = r'./MnistDataSets/mnist_train.csv'
testing_file_loc = r'./MnistDataSets/mnist_test.csv'
input_node_num = 784
hidden_node_num = 150
output_node_num = 10
learning_rate = 0.1
epochs = 2

# 实例化神经网络
n = NeuralNetwork.NeuralNetwork(input_node_num, hidden_node_num, output_node_num)

# 加载训练集csv文件
training_data_file = open(training_file_loc, 'r')
training_data_list = training_data_file.readlines()
training_data_file.close()

# 训练
for e in range(epochs):
    for training_data in training_data_list:
        all_values = training_data.split(',')
        # 从第二个元素开始是输入值 将其从[0, 255]映射到[0.01, 0.99]
        inputs = (numpy.asfarray(all_values[1:]) / 255.0 * 0.99) + 0.01
        # 第一个元素是数字的值 预期值为其它0.01 对应的为0.99
        targets = numpy.zeros(output_node_num) + 0.01
        targets[int(all_values[0])] = 0.99
        # 千训练
        n.train(inputs, targets, learning_rate)
        pass
    pass

# 测试
test_data_file = open(testing_file_loc, 'r')
test_data_list = test_data_file.readlines()
test_data_file.close()

score = 0
for test_data in test_data_list:
    all_values = test_data.split(',')
    correct_num = int(all_values[0])
    outputs = n.query((numpy.asfarray(all_values[1:]) / 255.0 * 0.99) + 0.01)
    output_num = numpy.argmax(outputs)
    if output_num == correct_num:
        score += 1
    else:
        print("输出错误：将", correct_num, "识别为", output_num)
        pass
    pass
print("分数：", score)

正确率在90%上。

保存、读取模型

每次测试都要测试一遍属实是没必要，所以实现一下训练后保存模型和读取模型测试的功能：

在神经网络类中加入获取和设置模型的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def get_model(self) -> tuple[numpy.ndarray, numpy.ndarray]:
    """
    获得模型矩阵

    :return: 模型的两个权重矩阵wih和who
    """
    return self.wih, self.who

def set_model(self, wih: numpy.ndarray, who: numpy.ndarray):
    """
    设置模型权重矩阵

    :param wih: 矩阵wih
    :param who: 矩阵who
    """
    self.wih = wih
    self.who = who
    pass

使用os和json库，将要存的转为json保存为txt文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import json
import os


save_dir = r'./Model'
save_name = '100_1_1.txt'

# 保存到文件
if not os.path.exists(save_dir):
    os.mkdir(save_dir)
    pass
with open(save_dir + '/' + save_name, 'w') as f:
    wih, who = n.get_model()
    save_data = {
        'input_num': input_node_num,
        'hidden_num': hidden_node_num,
        'output_num': output_node_num,
        'wih': wih.tolist(),
        'who': who.tolist()
    }
    json.dump(save_data, f)
    pass

读取也一样

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import json
import numpy
import NeuralNetwork


model_dir = r'./Model'
model_name = '200_03_7_Rot.txt'
testing_file_loc = r'./MnistDataSets/mnist_test.csv'

with open(model_dir + '/' + model_name, 'r') as f:
    json_data = json.load(f)
    input_node_num = json_data['input_num']
    hidden_node_num = json_data['hidden_num']
    output_node_num = json_data['output_num']
    wih = numpy.array(json_data['wih'])
    who = numpy.array(json_data['who'])
    pass

n = NeuralNetwork.NeuralNetwork(input_node_num, hidden_node_num, output_node_num)
n.set_model(wih, who)

测试

正确率测试

隐藏节点数量 学习率 epochs 正确率
100 0.1 1 95.2%
200 0.05 2 95.8%
200 0.05 4 97.3%
200 0.03 7 97.4%

可以达到97%以上的正确率，已经非常可观了。

反向查询

玩个好玩的：从输出层输入，反推出输入层，并显示为图像：

实现反向查询方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 反向查询
def back_query(self, targets):
    final_outputs = numpy.array(targets, ndmin=2).T
    final_inputs = self.inverse_activation_func(final_outputs)

    hidden_outputs = numpy.dot(self.who.T, final_inputs)
    hidden_outputs -= numpy.min(hidden_outputs)
    hidden_outputs /= numpy.max(hidden_outputs)
    hidden_outputs = hidden_outputs * 0.98 + 0.01
    hidden_inputs = self.inverse_activation_func(hidden_outputs)

    inputs = numpy.dot(self.wih.T, hidden_inputs)
    inputs -= numpy.min(inputs)
    inputs /= numpy.max(inputs)
    inputs = inputs * 0.98 + 0.01

    return inputs

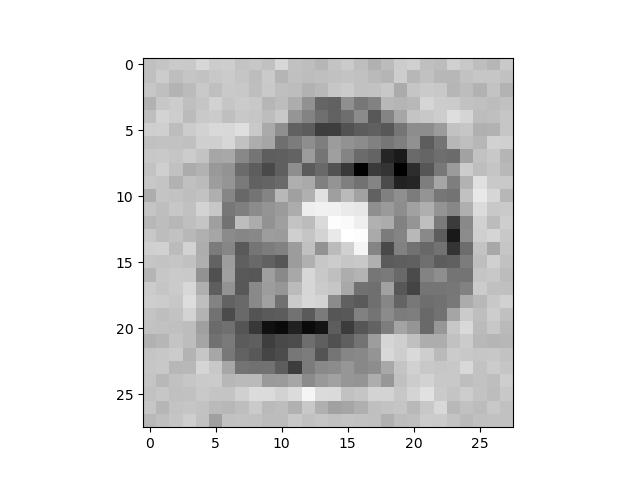
输入数字测试：

数字0

数字3

数字8

可以看出每个数字的特点，这就是神经网络识别数字的方式。

其它优化

旋转

将训练样本旋转正负10度进行训练：

1
2
3
4
5
# 用scipy的rotate方法旋转
input_rotate_image_1 = scipy.ndimage.rotate(inputs.reshape(28, 28), 10, cval=0.01, reshape=False)
input_rotate_image_2 = scipy.ndimage.rotate(inputs.reshape(28, 28), -10, cval=0.01, reshape=False)
n.train(input_rotate_image_1.reshape(784), targets, learning_rate)
n.train(input_rotate_image_2.reshape(784), targets, learning_rate)

GPU加速

尝试使用Taichi图形学库进行GPU加速测试。

遇到了不少问题：Taichi不自带大矩阵乘法库，得自己写矩阵乘法，且field不能作为参数传入函数，所以也不能自己实现矩阵乘法方法，只能一个一个乘。

不过最后总算是用各种方法实现了，不过也有很多可以优化的地方，可以参考下：

资源：https://github.com/1keven1/SimpleDigitalRecognitionNeuralNetwork/tree/master/Taichi

性能测试

刚写完一测试发现性能不升反降，给我吓得。还好在测试神经网络复杂度的时候有了眉目：

耗时与隐藏层节点数量的关系

100 200 300
numpy (s) 14.24 47.53 67.99
Taichi (s) 42.43 44.18 44.71

分析

经分析，我这个神经网络较为简单，在训练时单个样本的训练时间不长，只是样本多。

使用GPU训练时，GPU只并行了单个样本的训练，因此性能提升不明显；反之，由于每个样本都要将数据传入显存，在此处花费了大量时间，因此性能降低。

所以我将隐藏层节点数量调大，模拟更复杂的神经网络，果然随着神经网络复杂度的增加，CPU性能迅速降低，GPU性能则变化很小，因此对于更复杂的神经网络来说，GPU加速才有意义。

不过对于我这个数字识别的简单神经网络来说，隐藏节点数量在200以后就趋于收敛，更大对于模型正确率影响不大，所以这种GPU加速没有意义。

其它优化

可以考虑使用Batch Size的思路，一次在显存中读入多个样本数据，同时并行计算。

资源

训练集、测试集：https://pjreddie.com/projects/mnist-in-csv/

https://github.com/1keven1/SimpleDigitalRecognitionNeuralNetwork